Le compas digital

(Le compas digital : page mise à jour par Benjamin le 24 mars 2024)

Le compas magnétique, le chronomètre, le sextant et les cartes ont longtemps été les seuls instruments de navigation. Avec le loch dans la marine, puis l’anémomètre dans l’aéronautique, pour connaître la vitesse, et estimer la distance parcourue en fonction du temps écoulé. Certains avions de la seconde guerre mondiale étaient équipés d’un astrodôme pour permettre au radio-navigateur de faire le point astronomique au sextant. A la fin des années 50, Air France avait équipé ses Super Starliners d’un sextant périscopique !

La radionavigation, puis le GPS, ont eu raison de ces techniques de navigation quasi ancestrales. Mais la navigation aérienne à l’estime, à la montre et au compas, reste enseignée. Et c’est heureux, car au stade d’élève pilote, cette base est indispensable à l’acquisition d’une bonne représentation mentale du temps et de l’espace dans lesquels évoluent nos aéronefs. Le pilote qui a acquis un peu d’expérience conserve sa montre, mais il ne regarde plus beaucoup son compas magnétique. Sauf parfois pour se rassurer en pensant qu’il pourra compter sur lui en cas de panne de son GPS ou de sa tablette… à la condition d’avoir conservé les réflexes utiles de la navigation à l’estime !

Le compas magnétique traditionnel, hors obligation règlementaire, est donc devenu peu utile, voire obsolète pour certains. Mais il conserve un autre intérêt, dans sa version digitale, lorsqu’il est couplé à un calculateur et à un GPS. Par exemple pour indiquer précisément au pilote la direction et la vitesse du vent, grâce à un calcul faisant intervenir la vitesse de l’avion, la route géographique fournie par le GPS, et le cap fourni par le compas, corrigé de la déclinaison.

Le champ magnétique terrestre

Le champ magnétique terrestre est établi entre les pôles magnétiques nord et sud, lesquels ne sont pas confondus avec les pôles géographiques, d’où la déclinaison magnétique. Entre ces pôles magnétiques s’établissent des lignes de champ qui sont grossièrement comparables à celle d’un simple barreau aimanté, représenté en rouge sur la figure 1.

On voit sur cette représentation schématique que les lignes de champs sont grossièrement parallèles à la surface terrestre aux environs de l’équateur, perpendiculaires à cette surface aux environs des pôles magnétiques et plus ou moins inclinées en fonction de la latitude. Mais quelle que soit la localisation géographique, la projection d’une ligne du champ magnétique sur un plan parallèle à la surface terrestre est toujours orientée vers un pôle magnétique. C’est ce qui est à la base du principe de la boussole, un instrument qui doit toujours être horizontal pour prétendre indiquer la direction du pôle magnétique.

Le magnétomètre

Le cœur d’un compas digital est constitué d’un magnétomètre triaxial. Ce capteur particulier analyse le champ magnétique environnant, et le décompose en trois vecteurs, selon les trois axes orthogonaux x, y et z de son propre repère cartésien.

Il existe une très grande variété de magnétomètres. Ceux qui nous intéressent dans le cadre de ce site sont de type magnétorésistif. Cette technologie permet d’obtenir des capteurs précis, sensibles et fiables, de taille infra millimétrique. Ce sont eux qui équipent tous les smartphones du commerce. Ces capteurs sont très souvent associés à des accéléromètres et des gyromètres, au sein d’une IMU (Inertial Measurement Unit).

Si un magnétomètre est posé horizontalement sur une table, axe z vertical, les axes x et y de ce magnétomètre sont donc dans un plan horizontal, parallèle à la surface terrestre. Dans ce cas particulier, l’analyse des seules composantes x et y suffit pour calculer l’orientation magnétique du magnétomètre.

Mais dans un avion, le magnétomètre, fixé à la structure, ne peut pas toujours être à l’horizontale. Par conséquent, en évolutions, le calcul de l’orientation magnétique devra faire intervenir les 3 axes du magnétomètre, et intégrer l’attitude de l’avion en assiette et en inclinaison.

Dans le cadre de ce projet, nous avons choisi d’utiliser le capteur LIS3MDL de ST Microelectronics, sur une carte Adafruit. Ce capteur récent utilise le bus I2C ou le bus SPI pour communiquer. Plusieurs bibliothèques sont disponibles.

Le calibrage du magnétomètre

Le LIS3MDL est calibré en usine pour la sensibilité et le niveau zéro-gauss. Les facteurs correctifs sont stockés dans une mémoire non volatile, interne au capteur, et à chaque mise sous tension, ils sont chargés dans les registres internes pour être pris en compte durant l’utilisation. Ce calibrage particulier n’est donc pas à refaire par l’utilisateur.

Par contre, un calibrage particulièrement soigneux doit être réalisé par l’utilisateur, afin de prendre en compte l’environnement magnétique particulier du capteur, à son emplacement définitif dans l’avion. En effet, cet environnement peut perturber plus ou moins sévèrement le champ magnétique terrestre qui seul nous intéresse.

Il existe deux sources de perturbations magnétiques, dites fer-dur et fer-doux (hard iron and soft iron). Pour faire simple, fer dur désigne les objets qui produisent un champ magnétique, par exemple des aimants permanents ou des conducteurs où circule un courant électrique. Le fer doux désigne certains métaux comme le fer ou le nickel qui, bien que non aimantés, sont capables de dévier les lignes du champ magnétique terrestre.

Il existe sur Internet de très nombreux sites expliquant 1) la théorie de ces perturbations, 2) les techniques de calibrage, et 3) les méthodes de compensation. Sans entrer dans des théories mathématiques complexes, qui nous dépassent, nous allons simplement aborder de façon très pratique les points 2 et 3, ce qui pourra aider le lecteur à calibrer n’importe quel magnétomètre, c’est à dire déterminer les coefficients nécessaires à la compensation.

Puis nous expliquerons comment introduire ces coefficients de compensation dans un algorithme, afin d’obtenir un cap magnétique exact, malgré les perturbations fer dur et fer doux de l’environnement du magnétomètre. Charge à l’utilisateur de tenir ensuite compte de la déclinaison du lieu où il vole pour calculer le cap géographique.

Il va sans dire que la plus élémentaire des précautions consiste surtout à installer le magnétomètre dans l’avion le plus loin possible de toutes les sources de perturbations. Par exemple dans un saumon d’aile, à la condition qu’il n’y circule pas des courants intermittents de très forte intensité, par exemple pour alimenter des feux à éclats…

La procédure de calibrage

Dans cet exemple, l’outil qui sera utilisé pour calculer les coefficients de calibration est le logiciel Magneto 1.2, téléchargeable ici. Le fichier txt doit être formaté (par exemple avec NotePad++, ou n’importe quel logiciel de traitement de texte et la fonction “rechercher-remplacer”) pour contenir sur chaque ligne les valeurs du champ magnétique, respectivement sur les axes x, y et z, simplement séparées par un espace.

Une fois les données enregistrées, il suffit de lancer Magneto 1.2, et de lui indiquer l’emplacement du fichier texte à traiter. Plus d’explications ici, notamment pour la saisie à effectuer dans la case “Norm of Magnetic or Gravitational Field”. Il faut procéder par approximations successives, jusqu’à ce que la moyenne des 3 cases en diagonale entourées en rouge sur la copie d’écran ci-dessous (Fig. 2) soit la plus proche possible de 1.

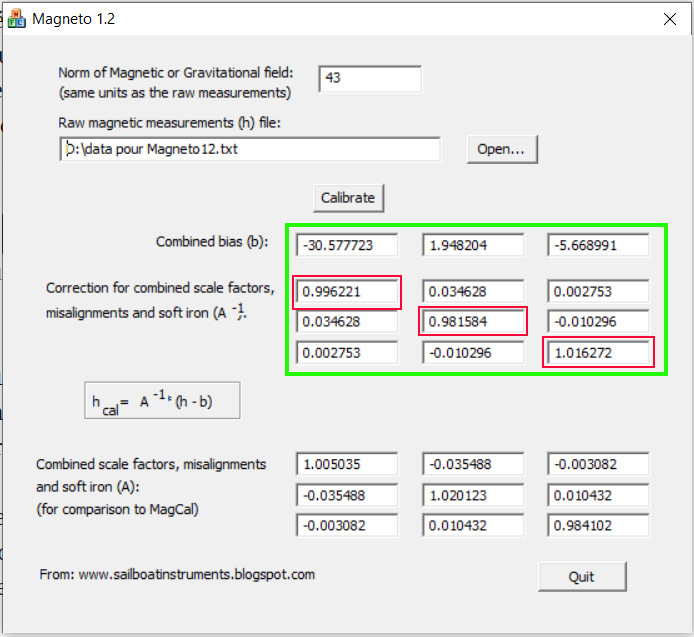
On a ainsi dans le cadre vert de la figure 2 tous les coefficients de calibrage qu’il faudra introduire à l’étape suivante dans le sketch exploitant le magnétomètre, afin de parfaitement compenser les distorsions fer dur et fer doux.

On peut obtenir ces coefficients avec un autre logiciel : MotionCal, téléchargeable ici. En fonction du système d’exploitation utilisé, et des éventuelles protections antivirus, MotionCal peut parfois être un peu “rétif” au téléchargement, sans doute parce qu’il s’agit d’un fichier exécutable hébergé sur une page non sécurisée du site PJRC (le fabricant des cartes Teensy). En copiant et collant l’URL de la page de téléchargement dans un nouvel onglet du navigateur, cela règle généralement la question.

(http://www.pjrc.com/teensy/beta/imuread/MotionCal.exe).

Le principe de MotionCal est légèrement différent. Ce logiciel exploite en temps réel les données du magnétomètre, reçues sur le port série, sans avoir besoin de les enregistrer dans un fichier. Il faut pour cela fermer le terminal de l’IDE Arduino, et indiquer dans MotionCal quel port série utiliser. Il s’agit de celui où est connecté la carte Arduino ou Teensy.

Le formatage de la sortie des données vers le port série est un peu plus compliqué qu’avec Magneto 1.2, car MotionCal est prévu pour recevoir les données d’une IMU 9 DOF (accéléromètre triaxial + gyromètre triaxial + magnétomètre triaxial). Si on prend la première ligne du fichier prévu pour Magnéto 1.2, à savoir : “-52.27 -8.07 -40.49”, son formatage pour MotionCal serait : “raw:0,0,0,0,0,0,523,81,405”. Les valeurs relevées sur les 3 axes du magnétomètre sont multipliées par 10 et arrondies à l’entier le plus proche, précédées par 6 zéros, et séparées par des virgules, avec le mot raw en début de chaque ligne.

L’exemple imucal.ino de la bibliothèque Adafruit pour le LIS3MDL met en œuvre ce formatage particulier. Lors des mouvements de rotation imprimés au magnétomètre pour le calibrage, on voit progressivement se dessiner une sphère dans la fenêtre graphique de MotionCal. Quand la sphère est complète et centrée, on peut arrêter la procédure, et relever les valeurs figurant dans le cadre vert, voir la figure 3.

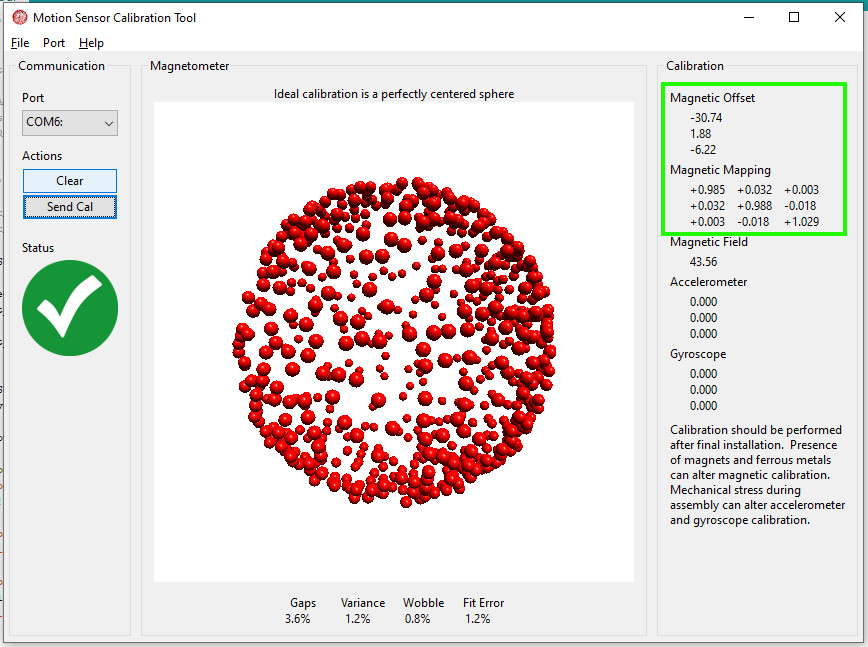
Les deux outils, Magnéto v1.2 et MotionCal, fournissent chacun deux matrices de nombres décimaux, leur comparaison montre que les deux logiciels fournissent des coefficients quasiment identiques. Il reste à exploiter ces coefficients dans le logiciel d’application utilisant le magnétomètre, de façon à réaliser la compensation fer dur et fer doux.

On peut bien sûr objecter à cette procédure de calibrage qu’elle ne concerne que le magnétomètre lui-même, avec l’éventuel microcontrôleur qui lui serait directement rattaché, ainsi que le boîtier qui protège l’ensemble, avec la connectique, mais avant fixation à la structure de l’avion. Cette dernière peut en effet générer également des perturbations magnétiques.

Mais il n’est généralement pas possible de faire tourner rapidement l’ensemble de l’avion sur ses trois axes, sauf évolutions serrées en voltige. D’où l’intérêt de choisir soigneusement l’emplacement du magnétomètre, le plus à distance possible des perturbations magnétiques.

Il est cependant possible de réaliser en vol un enregistrement des données brutes du magnétomètres, dans toutes les positions possibles de l’avion en fonction de son domaine de vol, et dans tous les azimuts. Après le vol, il faut soumettre cet enregistrement à Magneto 1.2 ou à MotionCal, pour voir si les coefficients ainsi obtenus sont différents de ceux obtenus en faisant simplement tourner manuellement le boîtier du magnétomètre comme décrit ci-dessus.

La procédure de compensation fer dur et fer doux

Pour appliquer les coefficients de calibration obtenus à l’étape précédente, il faut faire le produit d’une matrice 3×3 par une matrice 3×1. Le lecteur pourra se référer à un cours élémentaire de calcul matriciel (par exemple ici ou là) pour comprendre l’algorithme.

Le calcul à réaliser est le suivant :

où Xc, Yc et Zc sont les valeurs compensée, C11 à C33, ainsi que Cx, Cy et Cz sont les coefficients qui ont été calculés par MotionCal ou Magneto 1.2, et X, Y, et Z sont les valeurs brutes issues du magnétomètre.

Si on reprend par exemple les valeurs brutes citées plus haut, à savoir “-52.27 -8.07 -40.49” , et qu’on veut leur appliquer une compensation avec les coefficients de la figure 3, cela donne :

D’où :

Xc= 0,985 x (-52,27+30,74) + 0,032 x (-8,07-1,88) + 0,003 x (-40,49 + 6,22) = -21,63

Yc= 0,032 x ( -52,27+30,74 ) + 0,988 x ( -8,07-1,88 ) -0,018 x ( -40,49 + 6,22 ) = -9,90

Zc = 0,003 x ( -52,27+30,74 ) -0,018 x ( -8,07-1,88 ) + 1,029 x ( -40,49 + 6,22 ) = -35,15

Exemple du code correspondant :

#include <Adafruit_LIS3MDL.h>
Adafruit_LIS3MDL lis3mdl;
#define LIS3MDL_ADDRESS 0x1C

// Variables pour stocker les données brutes du magnétomètre
float magx, magy, magz;

// Données correctives issues de la calibration du magnétomètre. Ces données sont applicables à des mesures en µTesla.
float MagOffset[3] = {-30.74, 1.88, -6.22}; // Offsets pour les axes x, y et z
float mCal[3][3] = 
{
  {+0.985, +0.032, +0.003},
  {+0.032, +0.988, -0.018},
  {+0.003, -0.018, +1.029}
};

// Variables pour stocker les données magnétiques corrigées
float magxc, magyc, magzc;
float capmagnetique;

void setup() {
lis3mdl.begin_I2C(LIS3MDL_ADDRESS, &Wire1);
}

void loop() {
lis3mdl.read();      // Acquisition de X, Y et Z 
  magx = lis3mdl.x/68.42; //Conversion des données digitale brutes en µTesla
  magy = lis3mdl.y/68.42; //voir datasheet LIS3MDL p 8
                          // (https://www.st.com/resource/en/datasheet/lis3mdl.pdf)
  magz = lis3mdl.z/68.42;
  
// Calcul du produit des matrices
  magxc = mCal[0][0]*(magx-MagOffset[0])+ mCal[0][1]*(magy-MagOffset[1]) + mCal[0][2]*(magz-MagOffset[2]);
  magyc = mCal[1][0]*(magx-MagOffset[0])+ mCal[1][1]*(magy-MagOffset[1]) + mCal[1][2]*(magz-MagOffset[2]);
  magzc = mCal[2][0]*(magx-MagOffset[0])+ mCal[2][1]*(magy-MagOffset[1]) + mCal[2][2]*(magz-MagOffset[2]);

}

Le calcul du cap magnétique

Un fois le magnétomètre calibré, et les coefficients de calibration appliqués au valeurs brutes, on a les éléments pour calculer un cap magnétique.

Dans le cas le plus simple où le magnétomètre est strictement horizontal, l’axe z est vertical et sa composante de champ magnétique n’intervient pas dans le calcul. Le cap magnétique (en degrés, de 0 à 360) peut alors être obtenu très simplement par les deux lignes de code suivantes :

capmagnetique = atan2(magyc,magxc)*(180/PI);
if (capmagnetique<0) capmagnetique+=360;

Mais ce cas simple n’est pas adapté à l’avion où il faut prendre en compte les angles de roulis et de tangage, et donc la mesure selon l’axe z du champ magnétique. Dans un avion, les angles de roulis et de tangage sont transmis par l’AHRS de l’EFIS. Il ne faudrait pas se fier aux indications d’un simple accéléromètre, car en virage, la force centrifuge ne permettrait pas à ce dernier de fournir une référence verticale dans le repère terrestre.

Avant de calculer le cap magnétique, il faut donc préalablement effectuer un calcul de compensation pour les inclinaisons de l’avion selon les axes de roulis et de tangage (tilt compensation). Ce calcul permet de déterminer les deux composantes Xh et Yh dans un plan horizontal, en fonction des composantes triaxiales mesurées et calibrées plus haut Xc, Yc et Zc.

Les équations sont les suivantes :

Xh = Xc * Cos(pitch) + Zc * Sin(pitch)

Yh = Xc * sin(roll) * sin(pitch) + Yc * cos(roll) – Zc * Sin(roll) * Cos(pitch)

Et le code permettant d’obtenir un cap magnétique exact en fonction de l’attitude de l’avion et des données calibrées du magnétomètre devient donc:

Xh = magxc * cos(pitch) + magzc * sin(pitch);
Yh = magxc * sin(roll) * sin(pitch) + magyc * cos(roll) - magzc * sin(roll) * cos(pitch);
capmagnetique = atan2(Yh,Xh)*(180/PI);
if (capmagnetique<0) capmagnetique+=360;

La réalisation pratique du compas digital

Dans leur très grande majorité, les magnétomètres ont une sortie I2C et/ou SPI, tout comme le LIS3MDL. Ces interfaces ne sont pas prévues pour faire transiter des signaux sur une grande longueur. On a vu par ailleurs qu’un bon emplacement devait se trouver à distance des perturbations magnétiques, notamment celles liées au moteur et au tableau de bord.

Pour ces raisons, nous avons choisi d’associer, dans le même boîtier, le magnétomètre et un microcontrôleur. Ce dernier est chargé de transmettre les mesures au boîtier principal de l’EFIS, situé sur le tableau de bord, via un CAN bus. En effet, ce bus très rapide autorise les grandes longueurs, avec une excellent immunité face aux interférences électromagnétiques.

Le CAN Bus implémenté dans notre projet est particulièrement simple, il comporte pour l’instant seulement cinq nœuds, à savoir le module magnétomètre distant dont il est question sur cette page, le module EFIS, le module AHRS, l’EMS et le micro-EMS. Nous nous sommes donc affranchis des lourdes contraintes et préconisations du protocole CANaerospace.

L’emplacement choisi dans un saumon d’aile est également propice à l’installation d’un capteur de température et d’humidité. Ce dernier est nécessaire au calcul de l’altitude densité. Nous avons fait le choix du module Adafruit “SHT-30 Mesh-protected Weather-proof Temperature/Humidity Sensor”, product ID 4099.

La carte microcontrôleur est une Teensy 4.0, associée à un transceiver CAN bus MCP2562EP. Les connexions au CAN bus et au capteur de température et d’humidité se font par une prise SUB-D 9 broches.

Tout comme le module AHRS, le module compas digital doit être parfaitement aligné avec les trois axes de roulis, de tangage et de lacet de l’avion en ligne de vol horizontal rectiligne. Pour cela, dans un hangar ou au parking, il faut mettre l’installation électrique de l’avion sous tension, puis caler très précisément en hauteur les roues de l’avion pour que l’horizon artificiel soit parfaitement horizontal. Un simple niveau à bulle est alors suffisant pour caler le module magnétomètre horizontalement à 0.1° près en tangage comme en roulis (fig. 4).

L’orientation du module compas digital (fig. 5) est la suivante : les cartes Teensy et LIS3MDL sont sur le dessus, la LIS3MDL vers l’avant, et le connecteur D-SUB est à droite.

Résultats

Ce module distant, magnétomètre et capteur de température et d’humidité, a été testé en vol avec succès. Par rapport à l’EFIS Dynon monté sur le tableau de bord, les caps magnétiques sont identiques à plus ou moins 5 degrés, la température extérieure est identique à plus ou moins 0.5°C. L’altitude densité, dont le calcul fait appel à la température extérieure et à l’humidité relative, est plus difficilement comparable avec celle affichée par le Dynon qui ne comporte pas de capteur d’humidité, elle est généralement dans une fourchette de plus ou moins 250 pieds avec celle du Dynon, ce qui est parfaitement cohérent avec l’influence de l’humidité relative.