Les techniques de filtrage numérique d’un signal

(Dernière mise à jour le 25/12/2021)

En matière de traitement du signal, la fonction d’un filtre est de supprimer certaines partie du signal, comme par exemple le bruit.

La lecture périodique d’un capteur par un microcontrôleur fournit une série de valeurs au cours du temps, à une fréquence déterminée par le programme. Quels que soient le capteur, le microcontrôleur, le programme ou la fréquence d’échantillonnage, le signal obtenu est perturbé par ce qu’on appelle le bruit de mesure. Ce bruit peut être lié à des interférences extérieures ou à l’inévitable défaut de précision du capteur.

On rappelle que la précision d’un capteur traduit la dispersion des mesures autour d’une valeur moyenne. Son exactitude traduit la plus ou moins grande proximité de cette valeur moyenne avec la valeur réelle que l’on mesure. Dans la figure n°1 ci-dessous, la courbe bleue représente le signal à mesurer, tandis que la courbe rouge correspond à la mesure bruitée de ce signal par un capteur. On remarque que la mesure faite par ce capteur est entachée d’une nette imprécision. Mais elle a une bonne exactitude puisque la répartition des différentes mesures est centrée sur la valeur réelle du signal.

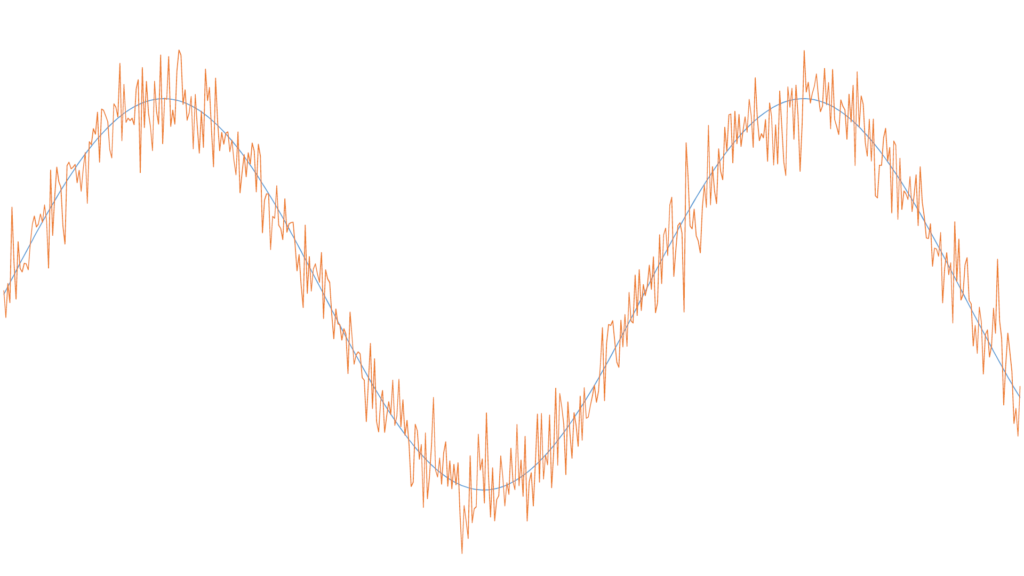
Le signal bruité de la figure n° 1 est très caractéristique de la problématique rencontrée en avionique. Qu’il s’agisse de la pression statique, de la température des culasses, du débit carburant, de la tension du bus principal, de l’angle d’inclinaison de l’avion, du taux de montée ou du régime moteur, les grandeurs mesurées évoluent généralement assez lentement. Le bruit de mesure a une fréquence nettement plus importante, qui est celle de la fréquence d’échantillonnage. La technique de lissage des courbes va donc faire appel à un filtre passe-bas. C’est à dire un filtre qui supprime les fréquences élevées. Le but du filtre est de corriger les mesures en temps réel. Cela permet de se rapprocher le plus possible de la courbe idéale correspondant au signal non bruité. Et d’afficher des valeurs stables et précises.

Pour atteindre ce but, deux techniques de filtre passe-bas sont utilisées dans les programmes de ce site. Le filtre à moyenne glissante, et le filtre à réponse impulsionnelle infinie (IIR filter en anglais, pour Infinite Impulse Response filter). Le sketch à télécharger ci-dessous illustre ces deux techniques. Il fonctionne sur toutes les cartes Arduino et Teensy. Dans le cadre de ce site web qui se veut avant tout pratique, il est hors de notre propos de présenter les théories mathématiques complexes du filtrage des signaux. Le lecteur qui le souhaite pourra par exemple consulter ce site, et bien d’autres.

Le filtre à moyenne glissante

Il consiste, pour chaque mesure, à faire le calcul de la moyenne arithmétique de la valeur actuelle et des N mesures précédentes. Cela suppose de garder en mémoire ces N mesures précédentes. On parle aussi de filtre à réponse impulsionnelle finie, car ce filtre est basé sur un nombre fini de valeurs du signal d’entrée. De façon générale, plus le nombre N est grand, meilleure est la qualité du lissage. Mais plus la mémoire utilisée pour stocker les dernières valeurs est importante. Et plus on va voir apparaître un retard de la courbe filtrée par rapport au signal (déphasage). Ce retard est facile à estimer. Il est égal au produit de la période d’échantillonnage par N/2. Si on échantillonne la grandeur à mesurer par exemple toutes les 50 ms, et qu’on fait une moyenne glissante sur 20 échantillons, le retard sera de 500 ms.

La figure n° 2 montre l’effet de ce filtre sur le même signal que celui de la figure n° 1, pour différentes valeurs de N. Si on souhaite utiliser ce type de filtre, il faut adapter le nombre N à l’amplitude du bruit : plus le bruit est important, plus N doit être grand pour un bon lissage, mais plus le déphasage sera net. Un inconvénient de ce filtre très efficace est la complexité (toute relative) de l’algorithme qui l’implémente. L’idéal est toujours de traiter un signal le moins bruité possible. Il est parfois possible d’améliorer la qualité du signal en changeant de modèle de capteur. Ou en agissant sur les interférences extérieures (blindage, boucles de masse, longueur des câbles, etc.).

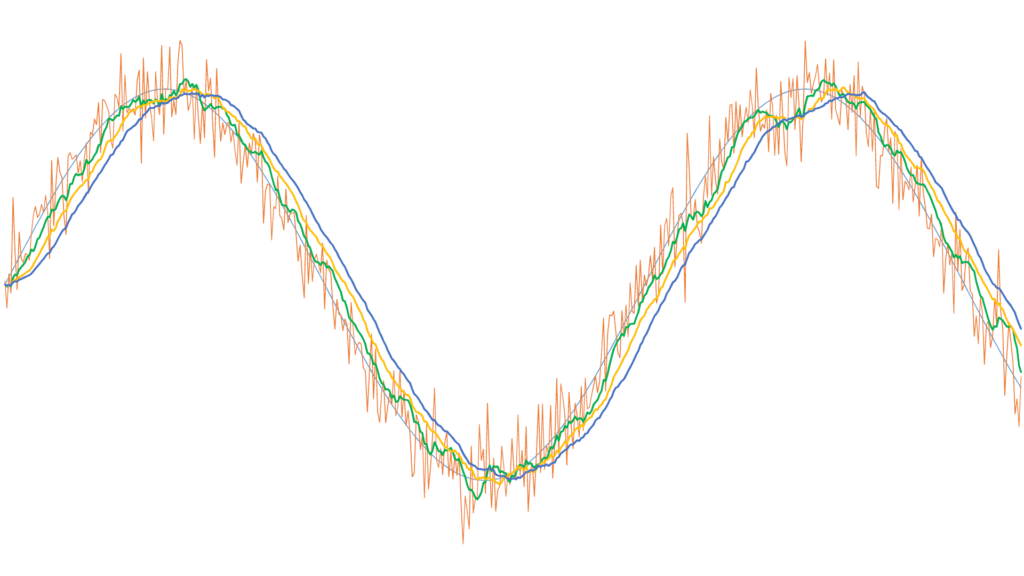
Le filtre à réponse impulsionnelle infinie

C’est un filtre récursif : pour chaque mesure, on fait intervenir dans son filtrage la valeur filtrée précédente, assortie d’un coefficient C, selon l’équation :

Valeur filtrée = valeur filtrée précédente * (1 – C) + valeur actuelle * C

On parle de réponse impulsionnelle infinie car toutes les valeurs précédentes, depuis le début du filtrage, ont en théorie une influence sur les futures valeurs filtrées. En pratique, cette influence devient rapidement négligeable avec le temps, sauf si le coefficient C est exagérément faible. Pour nos applications courantes en avionique, C est généralement compris entre 0,1 et 0,02. Les avantages de ce filtre sont la simplicité de sa programmation et son économie en ressources mémoire. Une seule valeur a besoin d’être mémorisée entre chaque échantillon. Comme pour le filtre à moyenne glissante, un déphasage apparaît. Il est d’autant plus important que le coefficient de filtrage diminue, avec comme corollaire une amélioration du filtrage. On voit sur la figure n° 3 le même signal bruité que sur les figures précédentes, traité par ce filtre récursif à réponse impulsionnelle infinie, avec différentes valeurs du coefficient C.

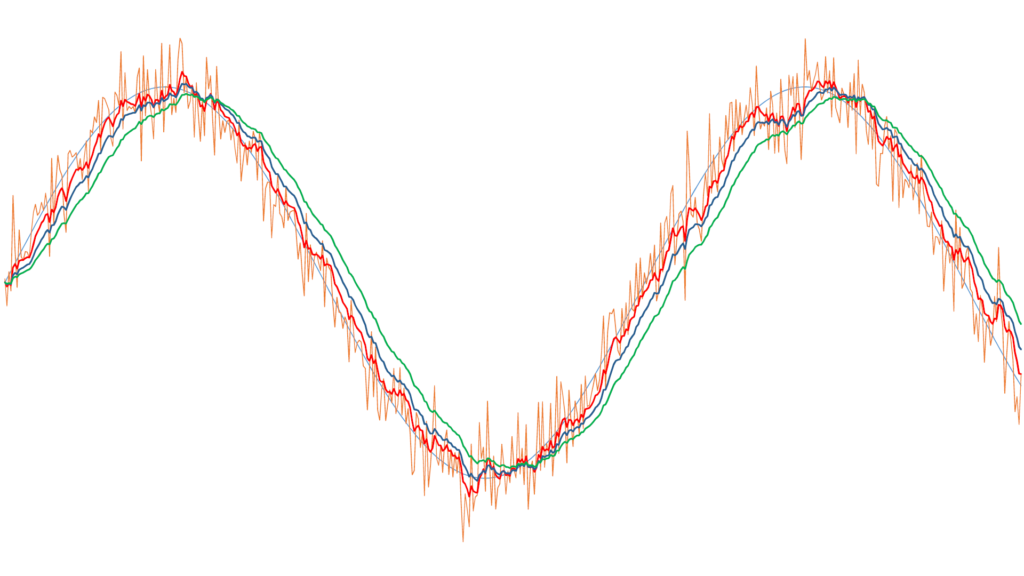
Comparaison entre ces deux filtres

Sur la figure n° 4, on a fait figurer toujours le même signal bruité, mais avec un filtrage par moyenne glissante sur 30 échantillons, et un filtrage IIR avec un coefficient à 0,06.

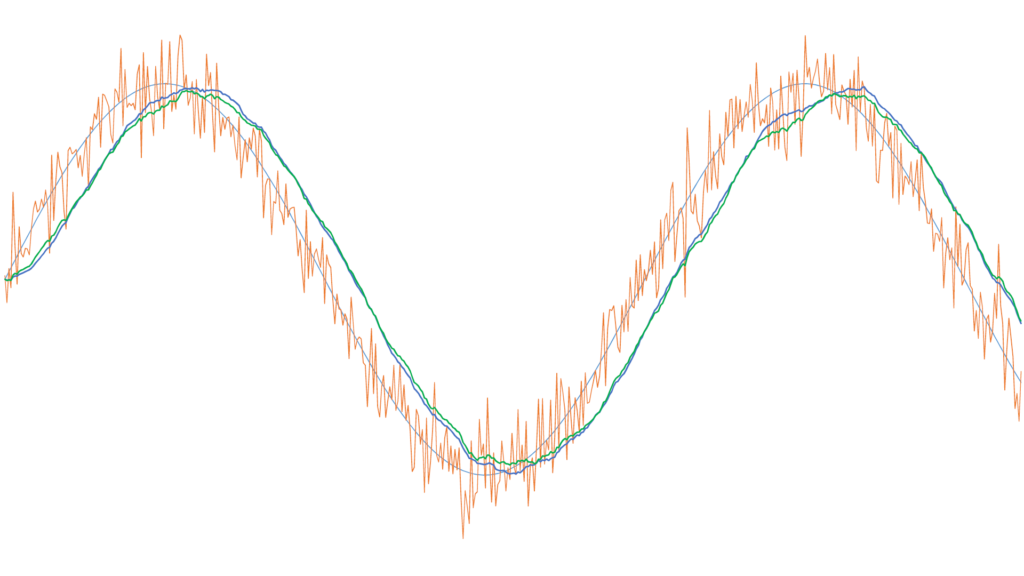
Que peut-on conclure de cette comparaison ? Pour ce signal très bruité, la figure n° 4 semble montrer un (très) petit avantage pour le filtre à moyenne glissante (courbe bleue). Le déphasage des deux courbes est sensiblement identique, mais d’une part la courbe bleue est un peu mieux lissée, mais surtout son amplitude est identique à cette du signal non bruité, alors que l’amplitude de la courbe verte est un peu “rabotée”. Le sketch en téléchargement plus haut permet de faire toutes les simulations que l’on souhaite pour comparer ces deux filtres. On peut faire varier le nombre d’échantillons pris en compte pour la moyenne glissante, le coefficient pour le filtre IIR, et même l’amplitude du bruit, en augmentant ou diminuant son écart type.

Le lecteur motivé pourra essayer d’autres filtres, en les rajoutant dans le même sketch. Par exemple le filtre de Kalman, pour lequel il existe des bibliothèques pour Arduino et Teensy, ici ou là.

De façon générale, pour choisir un filtre adapté et pour en régler les paramètres, la connaissance du signal à filtrer est importante. Un enregistrement en conditions réelles (en vol) ou simulées (en voiture) de ce signal sur une carte micro SD permet ensuite, à tête reposée, de tester différents filtres. Soit avec un tableur comme Excel, soit en “rejouant” le signal sur Arduino ou Teensy, et en observant les courbes sur le traceur série de l’IDE Arduino.