(Rotax temperature sensors, last updated by Gabriel on October 13, 2022)
Temperature sensor theory
Temperature sensors used in our aircrafts (especially on Rotax engines) are thermistors made of a negative temperature coefficient (NTC) semiconductor material.
Unlike metals, their resistance decreases with increasing temperature. The NTC thermistor’s Temperature- Resistance curve is described by the Steinhart-Hart Equation shown below:
1/T = A + B.Ln(R) + C.(Ln(R))3
(where T is the temperature in kelvins, and R is the resistance in ohms).
Sensors involved by this study
On Rotax engines, VDO brand sensors used for oil temperature, CHT, and waterless coolant temperature (fig. 1) are calibrated for a maximum temperature of 150°C (VDO part #323-057). For conventional coolant (non-waterless) temperature, a VDO sensor calibrated for 120°C (VDO part #323-095) is used.

The manufacturer of these sensors does not provide precise information on their characteristics. Therefore, we determined these characteristics by measuring the resistance of these two types of sensors as a function of temperature, from 50°C to 150°C.
Procedure
The sensor to be calibrated is immersed in a container filled with oil and heated to 160°C (fig. 2). Then, let cool, constantly stirring to homogenize the temperature. Using an ohmmeter and a digital thermometer previously calibrated against mercury laboratory thermometers, the sensor resistance is noted every 2 degrees, which gives the curve below (fig. 3).

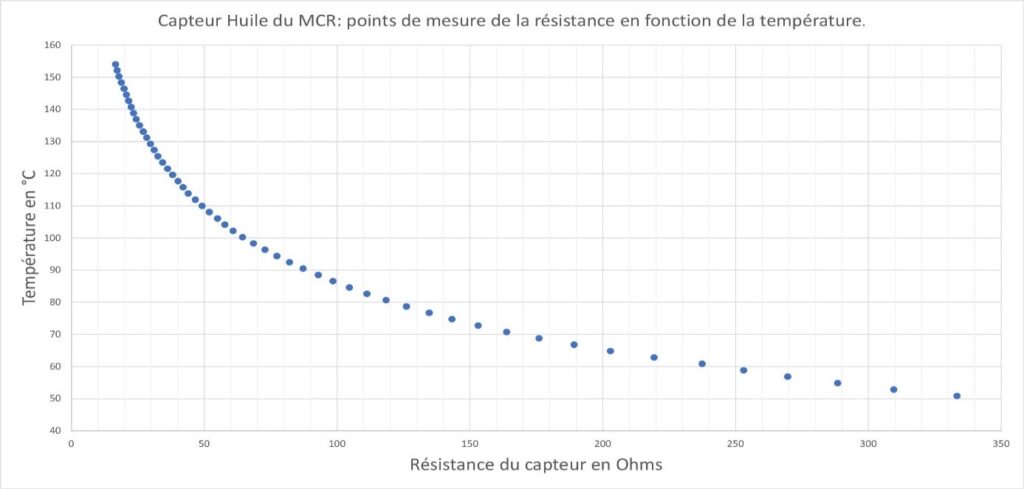
Mathematical modeling
The EMS (Engine Monitoring System) displays the engine parameters, including various temperatures. The EMS must first measure the resistance of the sensors and then calculate the corresponding temperature. Therefore, it is necessary to determine the formula the microcontroller can use to calculate these temperatures.
One could use the above formula of Steinhart-Hart, but determining its coefficients A, B, and C starting from experimental measurements is difficult.
An empirical method can give excellent results using a spreadsheet like Excel. The measurement points are plotted in semi-logarithmic coordinates: natural logarithm of the resistance on the horizontal axis and temperature on the vertical axis(fig 4).
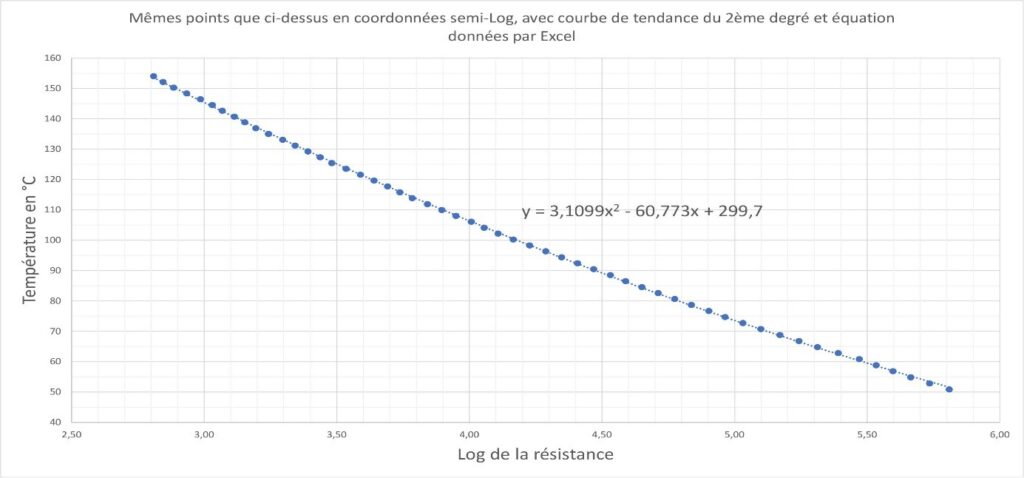
The curve then appears as a conic (polynomial of degree 2). Excel calculates the trendline and its equation shown on the graph (fig. 4). A replacement of the variables is made to obtain the desired formula:
t = A Log(R)2 + B Log(R) + C
The measurements on the two sensor types (VDO-150 and VDO-120) show that these sensors always have almost identical characteristics. A unique formula can perfectly characterize each of the two types.
By taking the average of several sensors of each type, we obtain the following curves and coefficients (fig. 5 and table 1):
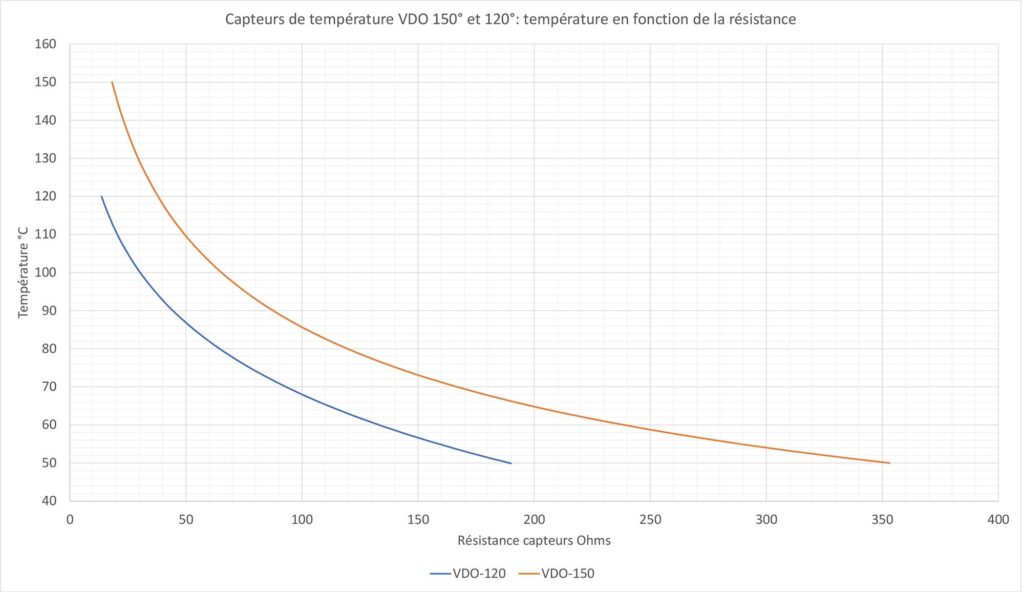
| | A | B | C |
| VDO-150 | 3,193 | -61,72 | 302,2 |
| VDO-120 | -0,796 | -20,39 | 178,8 |
